Question

`( \sin(x) + \tan(x) )/(1 + \sec(x) ) = \sin(x)`

how do I verify this problem?​

Answer 1

see explanation

Explanation:

Consider the left side

Simplify the numerator/denominator using the trigonometric identities

• tanx =
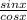`(sinx)/(cosx)` and secx =
`(1)/(cosx)`

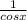
sinx + tanx = sinx +
`(sinx)/(cosx)` =
`(xsinxcosx+sinx)/(cosx)`

=
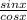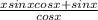
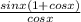`(sinx(1+cosx))/(cosx)` ← numerator

and

1 + secx = 1 +
`(1)/(cosx)` =
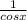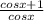`(cosx+1)/(cosx)` ← denominator

Putting this together gives

`(sinx(1+cosx))/(cosx)` ×
`(cosx)/(1+cosx)`

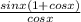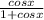
Cancel cosx and (1 + cosx) on numerator/ denominator, leaving

left side = sinx = right side ⇒ verified