Answer:
C. Minimum at (–3, –6)
Explanation:
The given expression is:
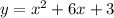
So, to complete the square, we first have to find the squared quotient between the second-term coefficient and 2, the add and subtract this number at the same time in the expression, like this:
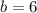

Then,
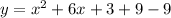
Now, we just have to group the terms that can be factorized:
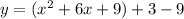
Then, the factorization would be made using the squared root of
 and
and
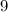 , which is:
, which is:

At the end, we just operate independent number outside the factorization:

So, according to the complete square of the expression, we can see that the vertex has coordinates
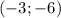 , which is a minimum, because the squared coefficient is positive, that means the parabola is concave up.
, which is a minimum, because the squared coefficient is positive, that means the parabola is concave up.
The reason why the vertex has that coordinates is because the explicit expression of a parabola is:
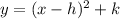
Where
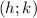 is vertex coordinates.
is vertex coordinates.
Therefore, the answer is C.