Answer:
The co-factors and their values are shown in the table below.
Explanation:
We are given the matrix,
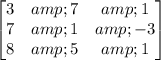 .
.
It is required to match the co-factors with the corresponding values.
As, the co-factors are given by,
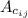 =
=
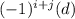 , where the d= determinant of the matrix after removing the i- row and j- column.
, where the d= determinant of the matrix after removing the i- row and j- column.
So, we have,
1.
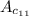 .
.
So,
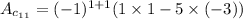
i.e.
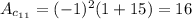
2.
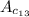 .
.
So,
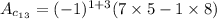
i.e.
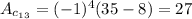
3.
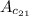 .
.
So,
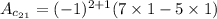
i.e.
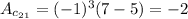
4.
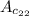 .
.
So,
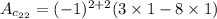
i.e.
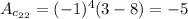
5.
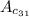 .
.
So,
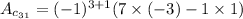
i.e.
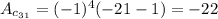
Thus, we get,
Co-factor Value
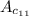 16
16
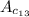 27
27
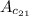 -2
-2
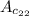 -5
-5
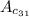 -22
-22