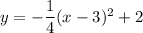Answer:
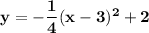
Explanation:
The vertex form of a quadratic equation is: y = a(x - h)² + k, where
- (h, k) is the vertex
- "a" is the vertical stretch
Input the vertex (3, 2) and the point (-1, -2) into the equation to solve for "a":
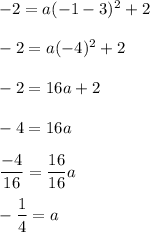
Now, input the vertex and the a-value into the equation: