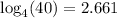Answer:
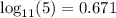 and
and
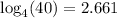
Explanation:
Given:
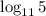 and
and
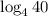
We have to rewrite each logarithm as a quotient of natural logarithms.
Using property of logarithm,
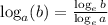
Consider 1)
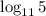
Applying property stated above,
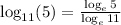
We have
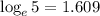 (approx)
(approx)
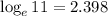 (approx)
(approx)
Substitute, we get,
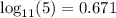
Consider 2)
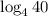
Applying property stated above,
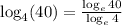
We have
 (approx)
(approx)
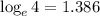 (approx)
(approx)
Substitute, we get,
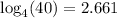
Thus,
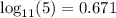 and
and