Answer:
B. x= 4
Explanation:
We know that,
The result for the intersection of the secant and the tangent is given by by the figure below,
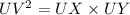
According to the question, we have,
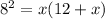
i.e.
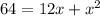
i.e.
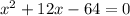
Now, the solution of a quadratic equation
 is given by,
is given by,
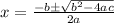
So, we get,
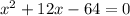 implies a= 1, b= 12 and c= -64.
implies a= 1, b= 12 and c= -64.
Thus, the solution is given by,
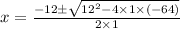
i.e.
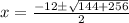
i.e.

i.e.
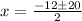
i.e.
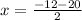 and i.e.
and i.e.
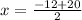
i.e.
 and i.e.
and i.e.
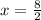
i.e x= -16 and x= 4.
Since, length cannot be negative.
So, we have, x= 4.