Question

There are 10 vehicles in a parking lot: 3 SUVs and 7 trucks. What is the probability that of any 7 randomly chosen vehicles, exactly 1 is an SUV? A. 0.142 B. 0.175 C. 0. 333 D. 0.428

Answer 1

B. 0.175

Explanation:

We are given that,

Total number of vehicles = 10

Number of SUV = 3

Number of trucks = 7

Probability to select any random 7 vehicles out of 100 is
`\binom{10}{7}`.

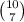It is required to select exactly 1 SUV.

Thus, we have, out of the 7 vehicles, exactly 1 is a SUV and other 6 are trucks.

So, the probability of selecting exactly 1 SUV is
`\frac{\binom{3}{1}* \binom{7}{6}}{\binom{10}{7}}`

i.e. Required probability =
`(3* 7)/((10* 9* 8)/(6))`

i.e. Required probability =
`(3* 7)/(10* 3* 4)`

i.e. Required probability =
`(21)/(120)`

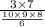
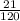
i.e. Required probability = 0.175

Hence, the probability to randomly select exactly 1 SUV from 7 vehicles is 0.175