Question

The graph of quadratic function f(x) has a minimum at (-2,-3) and passes through the point (2,13). The function g(x) is represented by the equation

g(x) = -(x+2)(x-3).

How much greater is the y-intercept of g(x) than f(x)?

Answer 1

ANSWER

The y-intercept of g(x) is 5 greater than f(x)?

EXPLANATION
The function f(x) has a minimum at (-2,-3) and passes through (2,13).
The equation in vertex form is given by,


`f(x)=a {(x - h)}^(2) + k`


`f(x)=a {(x + 2)}^(2) - 3`

We substitute (2,13) to find the value of a,


`13=a {(2 + 2)}^(2) - 3`


`a {(4)}^(2) = 16`


`a = (16)/(16)`


`a=1`


`f(x)={(x + 2)}^(2)-3`

The y-intercept is


`f(0)={( 2)}^(2) - 3 =1`

Also,


`g(x) = - (x + 2)(x - 3)`

has y-intercept,


`g(0) = - (0+ 2)(0 - 3) = 6`

The difference is


`6 -1= 5`

Answer 2

The y-intercept of g(x) is 5 greater than the y-intercept of f(x).

Explanation:

It is given that the graph of quadratic function f(x) has a minimum at (-2,-3) and passes through the point (2,13).

The equation of a quadratic function is

`f(x)=a(x-h)^2+k`

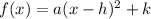
Where, (h,k) is vertex or extreme points and a is stretch factor.

The minimum value of function is (-2,-3), so the vertex is (-2,-3).

`f(x)=a(x-(-2))^2+(-3)`

`f(x)=a(x+2)^2-3`

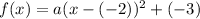
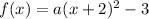
It is given that the function passing through the point (2,13).

`13=a(2+2)^2-3`

`16=16a`

`a=1`

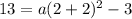
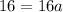
So, the function f(x) is

`f(x)=(x+2)^2-3`

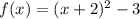
Substitute x=0, to find the y-intercept.

`f(x)=(0+2)^2-3`

`f(x)=4-3=1`

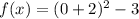
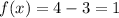
The y-intercept of f(x) is 1.

The given function is

`g(x)=-(x+2)(x-3)`

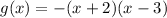
Substitute x=0, to find the y-intercept.

`g(x)=-(0+2)(0-3)=6`

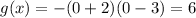
The y-intercept of g(x) is 6.

The difference between y-intercepts is

`6-1=5`

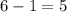
Therefore y-intercept of g(x) is 5 greater than the y-intercept of f(x).