Question

Find the area of the polygon WXYZ with its vertices at W(–3, –2), X(–3, 5), Y(2, 5), and Z(2, –2).

Answer 1

35

Explanation:

Answer 2

The area of the polynomial is 35 square unit.

Explanation:

It is given that area of the polygon WXYZ with its vertices at W(–3, –2), X(–3, 5), Y(2, 5), and Z(2, –2).

From the below graph it is noticed that the given polynomial is a rectangle with length 5 and width 7.

The distance formula

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

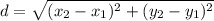
Using the above formula we get,

`WX=7`

`XY=5`

`YZ=7`

`WZ=5`

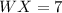
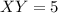
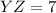
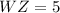
The length of opposing sides are equal.

Using the Pythagoras theorem, the length of diagonal WY and XZ are

`WY=√((WX)^2+(XY)^2)=√(7^2+5^2)=√(74)`

`XZ=√((XY)^2+(YZ)^2)=√(5^2+7^2)=√(74)`

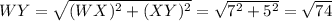
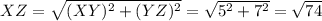
Since the length of the diagonal are same, therefore the given polygon is a rectangle.

The area of a rectangle is

`A=l* w`

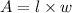
Where l is length and w is width.

The area of given polynomial is

`A=5* 7`

`A=35`

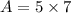
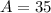
Therefore the area of the polynomial is 35 square unit.