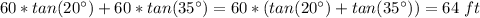Question

two buildings are 60 feet apart across a street. A person on top of the shorter building finds the angle of elevation of the roof of the taller building to be 20 degrees and the angle of depression of its base to be 35 degrees. How tall is the taller building to the nearest foot?

Answer 1

Explanation:

Let
`h_(1)` be the difference in heights of the building and
`h_(2)` be the height of the smaller building.

Let H be the Height of the taller building and the angle of elevation =20° and the angle of depression =35°.

Then,

⇒
`tan20^(\circ)+tan35^(\circ)=(h_(1)+h_(2))/(D)`

⇒
`0.363+0.700=(h_(1)+h_(2))/(D)`

⇒
`1.063=(H)/(D)`

⇒
`1.063{*}60=H`

⇒
`H=63.89 feet`

Therefore, the of the taller building =63.89 feet.

Answer 2

The height of the taller building is
`64\ ft`

Explanation:

see the attached figure to better understand the problem

step 1

Find the value of h1

with the angle of elevation

we know that

`tan(20\°)=(h1)/(60)`

`h1=60*tan(20\°)`

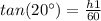
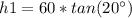
step 2

Find the value of h2

with the angle of depression

we know that

`tan(35\°)=(h2)/(60)`

`h2=60*tan(35\°)`

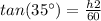
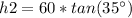
step 3

Find the height of the taller building

The height of the taller building is the sum of h1 plus h2

so

`60*tan(20\°)+60*tan(35\°)=60*(tan(20\°)+tan(35\°))=64\ ft`