Question

A ship of unknown heightis sighted from a lighthouse. From the top of the lighthouse, the angle of depression to the top of the mast and the base of the ship equals 30oand 45orespectively. If the shipis 50m away from the base of the lighthouse then what is the height of the ship(in meters)?

Answer 1

Explanation:

From the given information, consider DB=x be the height of the ship, BC= 50 m, then DE=50 m.

Now, From ΔABC,

`(AC)/(BC)=tan45^(\circ)`

⇒
`AC=50 m`

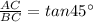
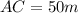
Also, from ΔADE, DE=50 m, we have

`(AE)/(DE)=tan30^(\circ)`

⇒
`(AE)/(50)=(1)/(√(3))`

`AE=(50)/(√(3))`

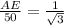
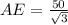
Now, AC=AE+EC

⇒
`50=(50)/(√(3))+EC`

⇒
`EC=50-(50)/(√(3))`

⇒
`EC=50-(50)/(1.732)`

⇒
`EC=50-28.86=21.14 m`

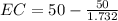
Also, we know that EC=BD, therefore BD=21.14 meters.

Thus,the height of the ship= 21.14 meters.