Answer:
Either
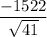 (approximately
(approximately
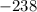 ) or
) or
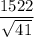 (approximately
(approximately
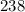 .)
.)
Explanation:
Let
 denote the first term of this geometric series, and let
denote the first term of this geometric series, and let
 denote the common ratio of this geometric series.
denote the common ratio of this geometric series.
The first five terms of this series would be:
First equation:
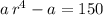 .
.
Second equation:
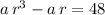 .
.
Rewrite and simplify the first equation.
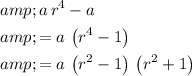 .
.
Therefore, the first equation becomes:
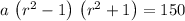 ..
..
Similarly, rewrite and simplify the second equation:
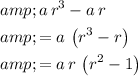 .
.
Therefore, the second equation becomes:
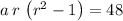 .
.
Take the quotient between these two equations:
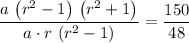 .
.
Simplify and solve for
 :
:
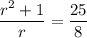 .
.
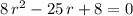 .
.
Either
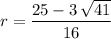 or
or
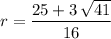 .
.
Assume that
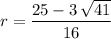 . Substitute back to either of the two original equations to show that
. Substitute back to either of the two original equations to show that
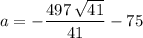 .
.
Calculate the sum of the first five terms:
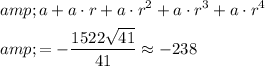 .
.
Similarly, assume that
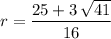 . Substitute back to either of the two original equations to show that
. Substitute back to either of the two original equations to show that
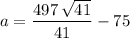 .
.
Calculate the sum of the first five terms:
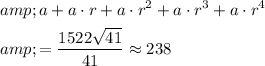 .
.