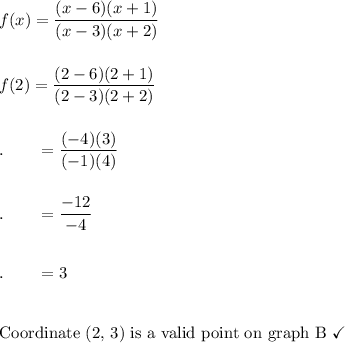Question

PLEASE HELP ASAP!!! CORRECT ANSWER ONLY PLEASE!!!

Which graph represents the function?

Answer 1

Answer: (C) bottom left graph

Explanation:

First, find the Vertical Asymptotes (VA) - which are the restrictions on the x-value. Since the denominator cannot be equal to zero, factor the denominator and set each factor equal to zero to find the VA asymptotes.

`f(x)=(x^2-5x-6)/(x^2-x-6)\\\\.\quad =((x-6)(x+1))/((x-3)(x+2))\\\\\\x-3=0\qquad x+2=0\\.\qquad x=3\qquad \quad x=-2\\\\\text{The Vertical Asymptotes are at x=3 and at x=-2}\\\text{The only graphs that satisfy this are graphs B and C}.`

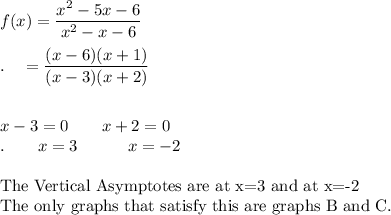
Next, find the Horizontal Asymptotes (HA) - which are the restrictions on y. This is determined by the degrees of the numerator and denominator. Since they have the same degree, the HA is the the coefficient of the numerator divided by the coefficient of the denominator.

`y=(1(x^2))/(1(x^2))\\\\y=1\\\\\text{The horizontal asymptote is y=1}\\\text{Check to see if the graph crosses the HA at y = 1}.\\\\1=(x^2-5x-6)/(x^2-x-6)\\\\x^2-x-6=x^2-5x-6\\\\-x-6=-5x-6\\\\4x-6=-6\\\\4x=0\\\\x=0\\\\\text{So the graph crosses the HA at (0, 1)}\\\text{The graphs that satisfy the HA and intersection at (0, 1) are graphs A, C, and D}`

The only graph that satisfies both the VA and HA is graph C.

Check: Choose an x-value and solve for "y" to verify that coordinate is on graph C. I choose x = 2

`f(x) = ((x-6)(x+1))/((x-3)(x+2))\\\\\\f(2) = ((2-6)(2+1))/((2-3)(2+2))\\\\\\.\qquad=((-4)(3))/((-1)(4))\\\\\\.\qquad=(-12)/(-4)\\\\\\.\qquad=3\\\\\\\text{Coordinate (2, 3) is a valid point on graph B}\ \checkmark`