The length of
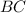 is 10 units.
is 10 units.
To solve for the length of
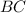 in the triangle provided in the image, we'll follow these steps:
in the triangle provided in the image, we'll follow these steps:
1. Recognize the type of triangle: Since two angles are given as 61 degrees each, and the sum of angles in any triangle is 180 degrees, we can find the third angle.
2. Use the third angle to determine the type of triangle: If the third angle is also 61 degrees, then the triangle is equilateral, and all sides are equal. If it's different, then the triangle is isosceles.
3. Apply properties of the specific type of triangle to solve for
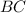 .
.
Let's start by calculating the third angle:
The sum of angles in a triangle is 180 degrees. Therefore, if we have two angles of 61 degrees each, the third angle
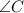 is:
is:
![\[ \angle C = 180^\circ - 61^\circ - 61^\circ \]](https://img.qammunity.org/2020/formulas/mathematics/high-school/ah7hhcrc2cahwa3qqoxxns41i8ek61fqna.png)
Now, let's calculate
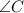 :
:
![\[ \angle C = 180^\circ - 122^\circ \]](https://img.qammunity.org/2020/formulas/mathematics/high-school/b8fvwgkdcr8abr10tmpnvuk4r3i94nf4sg.png)
![\[ \angle C = 58^\circ \]](https://img.qammunity.org/2020/formulas/mathematics/high-school/53a0v3s3ewd3lz7q519k995o8e6sggfg1p.png)
Since
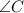 is not equal to the other two angles, the triangle is not equilateral; it is an isosceles triangle with angles
is not equal to the other two angles, the triangle is not equilateral; it is an isosceles triangle with angles
 and
and
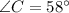 .
.
In an isosceles triangle, the sides opposite equal angles are also equal. Therefore, the lengths opposite
 and
and
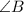 are equal, which are represented by
are equal, which are represented by
 and
and
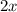 .
.
We can set up the equation:
![\[ 3x - 5 = 2x \]](https://img.qammunity.org/2020/formulas/mathematics/high-school/u7qll85p5qzm5asp3ox6oyepayjg7phd7v.png)
Now, let's solve for
 to find the length of
to find the length of
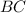 , which corresponds to
, which corresponds to
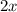 :
:
![\[ 3x - 2x = 5 \]](https://img.qammunity.org/2020/formulas/mathematics/high-school/7yr5fq9414f5ppdt6yepvfmgkzsjzb5js9.png)
![\[ x = 5 \]](https://img.qammunity.org/2020/formulas/mathematics/high-school/8sje1bbgbz11h6qnn1qylksc27z9xl4e98.png)
Thus, the length of
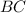 is:
is:
![\[ BC = 2x \]](https://img.qammunity.org/2020/formulas/mathematics/high-school/uo4qmtp58op9gt7yldupj4fpdvs6z1oyvh.png)
![\[ BC = 2 * 5 \]](https://img.qammunity.org/2020/formulas/mathematics/high-school/p3r1uodjappfy0kjm8659y12ozli8wdxtu.png)
![\[ BC = 10 \]](https://img.qammunity.org/2020/formulas/mathematics/high-school/197qejql5e9uwxrcbd7y04a6hz6jziqcrn.png)
So, the answer is 10 units.