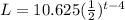Answer: Medication in Lexi's system on day t becomes,
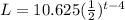
Explanation:
Since we have given that
Initial amount Sofia takes of a medicine = 10 mg
Concentration in blood decreases by a factor of one half every day.
So, it becomes,

According to question, four days later, it becomes,
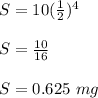
We have given that Lexi takes 10 mg of the same medicine.
So, it becomes,
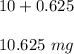
Hence, Medication in Lexi's system on day t becomes,