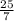Answer:
Explanation:
Given: △ACM, m∠C=90°, CP ⊥ AM , AC:CM=3:4, MP-AP=1.
Solution: Let AC=3k and CM=4k, then from △ACM, we get
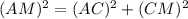
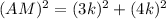
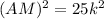
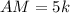
Now, AM=MP+AP⇒5k=MP+AP (1)
It is also given that MP-AP=1 (2)
Therefore, from (1) and (2),
(MP+AP)(MP-AP)=5k
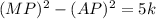
Add and subtract
 on left side
on left side
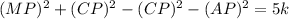
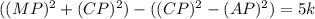 (3)
(3)
But, since CP ⊥ AM, Δ CMP and Δ CAP are right triangles. Therefore,
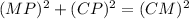
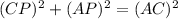
Thus, Equation (3) becomes,
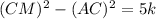
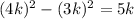
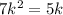
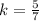
Thus, AM=5k
⇒AM=