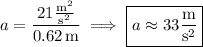Question

A 0.17 kg steel ball is tied to the end of a string and then whirled in a vertical circle at a constant speed v . The length of the string is 0.62 m , and the tension in the string when the ball is at the top of the circle is 4.0 N . What is v ?

What is the magnitude of the centripetal acceleration of the weight at this speed?

Answer 1

At the top of the circle, the net force on the ball is pointing downward, so that by Newton's second law

`\sum F = -ma \implies F_(\rm tension) + F_(\rm weight) = \frac{mv^2}R`

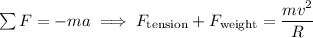
where
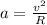`a=\frac{v^2}R` because the ball is undergoing circular motion with constant speed.

Plug in everything you know and solve for
`v`.

`4.0\,\mathrm N + (0.17\,\mathrm{kg}) g = \frac{(0.17\,\mathrm{kg})v^2}{0.62\,\rm m} \\\\ \implies v^2 = (0.62\,\rm m)/(0.17\,\rm kg) \left(4.0\,\mathrm N + (0.17\,\mathrm{kg}) g\right) \\\\ \implies v^2 \approx 21 (\mathrm m^2)/(\mathrm s^2) \implies \boxed{v \approx 4.5(\rm m)/(\rm s)}`

Plug this into the acceleration equation and solve for
`a`.

`a = (21(\mathrm m^2)/(\mathrm s^2))/(0.62\,\rm m) \implies \boxed{a \approx 33(\rm m)/(\mathrm s^2)}`