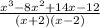Question

SOMEONE HELP!

add and simplify to find the answer for #15 and #12.
please provide answers are both not sure if number 12 is correct and explain why!?

Answer 1

see explanation

Explanation:

12

Since the denominators are like, add the numerators leaving the denominator

=
`(x+4+x-1)/(x-2)`

=
`(2x+3)/(x-2)`

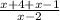
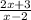
15

We require the denominators to be like before we can add.

factor x² - 4 as a difference of squares

x² - 4 = (x + 2)(x - 2)

Expressing as

`(x^2-6x)/(x+2)` +
`(2x-12)/((x+2)(x-2))`

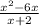multiply the numerator/denominator of the first fraction by (x - 2)

=
`((x-2)(x^2-6x))/((x+2)(x-2))` +
`(2x-12)/((x+2)(x-2))`

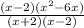Expand and simplify the numerators, leaving the denominator

=
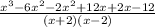
`(x^3-6x^2-2x^2+12x+2x-12)/((x+2)(x-2))`

=
`(x^3-8x^2+14x-12)/((x+2)(x-2))`