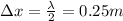Question

Two loudspeakers in a 20c room emit 686 hz sound waves along the x-axis.a. if the speakers are in phase, what is the smallest distance between the speakers for which the interference of the sound waves is perfectly destructive?b. if the speakers are out of phase, what is the smallest distance between the speakers for which the interference of the sound waves is maximum constructive?

Answer 1

1.

Answer:

`\Delta x = 0.25 m`

Step-by-step explanation:

Initially the two sound producing speakers are in same phase.

so here the distance between them must be equal to the half of the wavelength.

So here we will have

`f = 686 hz`

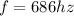
speed of sound wave

`v = 340 m/s`

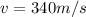
now we have

`\lambda = (v)/(f)`

`\lambda = (340)/(686) = 0.496 m`

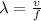
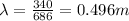
now the distance between two sources for destructive interference will be given as

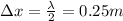
`\Delta x = (\lambda)/(2) = 0.25 m`

2.

Answer:

`\Delta x = 0.25 m`

Step-by-step explanation:

Initially the two sound producing speakers are out of phase.

so here the distance between them must be equal to the half of the wavelength for producing constructive interference.

So here we will have

`f = 686 hz`

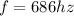
speed of sound wave

`v = 340 m/s`

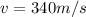
now we have

`\lambda = (v)/(f)`

`\lambda = (340)/(686) = 0.496 m`

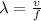
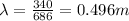
now the distance between two sources for constructive interference will be given as

`\Delta x = (\lambda)/(2) = 0.25 m`