Question

What is the measure of angle x

Angels are not necessarily drawn to scale

Answer 1

`\boxed{\boxed{\sf \angle x=76^(\circ)}}`

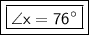
Explanation:

Given the diagram, we can see that ∠DIJ and ∠AIC are supplementary angles because they form a straight line.

∠DIJ and ∠JIC =180°

`\sf \angle DIJ+ 107=180`

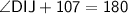
Subtract 107 from both sides:

`\sf \angle DIJ+107-107=180-107`

`\sf \angle DIJ=73`

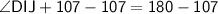
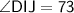
*Interior angles of a triangle always add up to 180*

`\sf \angle JDI+\angle DIJ+\angle DJI=180^(\circ)`

`\sf 31^(\circ)+73^(\circ)+\angle DJI=180^(\circ)`

`\sf \angle DIJ=76^(\circ)`

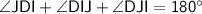
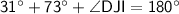
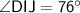
∠DJI and ∠x are vertical angles, therefore they are congruent.

∠x=76°

________________________________