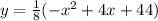Answer:
Equation of the parabola is
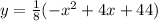
Explanation:
In this question the given focus is (2,4) and a directrix of y = 8 and we have to derive the equation of the parabola.
Let (x,y) is a point on the given parabola.Then the distance between the point (x,y) to (2,4) and the distance from (x,y) to diractrix will be same.
Distance between (x,y) and (2,4)
= √(x-2)²+(y-4)²
And the distance between (x,y) and directrix y=8
= (y-8)
Now √(x-2)²+(y-4)² = (y-8)
(x-2)²+(y-4)² = (y-8)²
x²+4-4x+y²+16-8y = y²+64-16y
x²+20+y²-4x-8y = y²-16y+64
x²+20-4x-8y+16y-64=0
x²+8y-4x-44 = 0
8y = -x²+4x+44