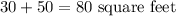Question

Please help me find out what k is.

Answer 1

Answer: a) k=8

b) The area of the addition =
`30\text{ square feet}`

The area of the entire patio after addition
`=80\ \text{square feet}`

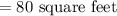
Explanation:

Given: The area of the patio before addition = 50 square feet

The area of the addition portion is given by
`k^2-3k-10`

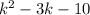
We can see that dimension of the total portion is
`k*(k+2)`

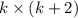
therefore, the area of the patio with the addition portion =
`k*(k+2)=k^2+2k`

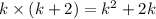
According to the question we have,

`k^2-3k-10+50=k^2+2k\\\Rightarrow-3k+40=2k\\\Rightarrow\ 5k=40\\\Rightarrow\ k=8`

Therefore, The area of the addition =
`8^2-3(8)-10=64-24-10=30\text{ square feet}`

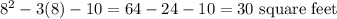
The area of the entire patio after addition =
`30+50=80\ \text{square feet}`