Answer: b. b^9
Explanation:
1. You can rewrite
![\sqrt[3]{b^(27)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/34dp9f0zs5pgtfp7qen504u3f0r783rtwl.png) as following:
as following:
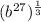
Because, by definition
![\sqrt[n]{x}=x^{(1)/(n)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/r0cusxq3yatmnt6bkuarb8a7kr4bhfsy9u.png)
2. Now, keeping on mind the exponents properties, you can multiply the exponents, then you obtain:
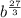
3. Finally, you must simplify the exponent, then, you obtain the following result:
