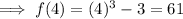Question

Hell don’t understand homework If f(x)=
5x-1

Answer 1

(a) -1

(b) 4

(c) 14

(d) 61

Explanation:

A piecewise function is a function which has different definitions for different intervals of x.

Given:

`f(x)=\begin{cases}5x-1 \quad \textsf{if }-5\leq x \leq 3\\x^3-3 \quad \textsf{if }\:\:\:\:\:\:3 < x \leq 4\end{cases}`

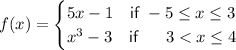
f(x) has 2 definitions:

Definition 1

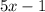`5x-1` when x is more than or equal to -5 and less than or equal to 3. This is a linear function.

Definition 2

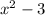`x^2-3` when x is more than 3 and less than or equal to 4. This is a cubic function.

Part (a)

We have to find f(0), so when x = 0.

x = 0 satisfies the condition -5 ≤ x ≤ 3 so the corresponding function is

`f(x)=5x-1`

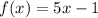
Substitute x = 0 in this definition:

`\implies f(0)=5(0)-1=-1`

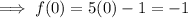
Part (b)

We have to find f(1), so when x = 1.

x = 1 satisfies the condition -5 ≤ x ≤ 3 so the corresponding function is

`f(x)=5x-1`

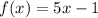
Substitute x = 1 in this definition:

`\implies f(0)=5(1)-1=4`

Part (c)

We have to find f(3), so when x = 3.

x = 3 satisfies the condition -5 ≤ x ≤ 3 so the corresponding function is

`f(x)=5x-1`

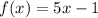
Substitute x = 3 in this definition:

`\implies f(0)=5(3)-1=14`

Part (d)

We have to find f(4), so when x = 4.

x = 4 satisfies the condition 3 < x ≤ 4 so the corresponding function is

`f(x)=x^3-3`

Substitute x = 4 in this definition:

`\implies f(4)=(4)^3-3=61`