Question

X² + 4y² = 36
The major axis runs along:
A) y=4x
B) x-axis
C) y-axis

Answer 1

The major-axis runs along the x-axis.

Explanation:

Answer 2

Option B - x-axis.

Explanation:

Given : Equation
`x^2+4y^2=36`

To find : The major axis runs along?

Solution :

The given equation is an ellipse the general form of an ellipse is

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

Converting into general form of an ellipse,

`x^2+4y^2=36`

Divide by 36 both side,

`(x^2)/(36)+(4y^2)/(36)=(36)/(36)`

`(x^2)/(36)+(y^2)/(9)=1`

`(x^2)/(6^2)+(y^2)/(3^2)=1`

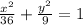
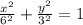
Here, a=6 and b=3

Since, a>b then the major axis of the ellipse is parallel to the x-axis.

Therefore, The major axis runs along x-axis of the equation
`x^2+4y^2=36`

So, Option B is correct.