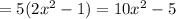Question

Given the functions, f(x) = 2x^2 - 1 and g(x) = 5x, Find f(g(x)) and g(f(x)).

Answer 1

`f ( g (x))`
`=2(5x)^2-1=2(25x^2)-1=50x^2-1`

`g ( f (x))`
`= 5(2x^2-1) = 10x^2-5`

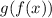
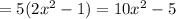
Explanation:

We are given the following functions and we are to find
`f ( g ( x ))` and
`g ( f ( x ))`.

`f (x) = 2x ^ 2 - 1`

`g (x) = 5 x`

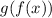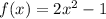
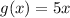
Finding [ tex ] f ( g (x)) [/tex] by substituting
`5x` in place of
`x`:

[ tex ] f ( g (x)) [/tex]
`=2(5x)^2-1=2(25x^2)-1=50x^2-1`

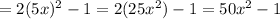
Now finding [ tex ] g ( f (x)) [/tex] by substituting
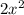`2x^2` in place of
`x`:

[ tex ] g ( f (x)) [/tex]
`= 5(2x^2-1) = 10x^2-5`

Answer 2

f(g(x)) = 50x^2 -1

g(f(x)) = 10x^2 - 5

Explanation:

Given: f(x) = 2x^2 -1 and g(x) = 5x

f(g(x)) = f.g(x)

Here we have to replace x by 5x in f(x) function

= 2(5x)^2 - 1

= 2(25x^2) - 1

f(g(x)) = 50x^2 -1

Now we have to find g(f(x))

We have to replace x by 2x^2 - 1 in g(x) function.

g(f(x)) = 5(2x^2 - 1)

g(f(x)) = 10x^2 - 5

Thank you.

Hope you will understand the concept.

Thank you.