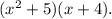Question

Which shows one way to determine the facts of x3+4x2+5x+20 by grouping

Answer 1

x^2(x+4) + 5(x + 4)

(x^2 + 5)(x + 4)

Answer 2

`x^(2)(x+4)+5(x+4)\\(x^(2) +5)(x+4).`

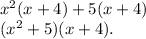
Explanation:

In order to be able to determine the facts of
`x^(3)+4x^(2)  +5x +20`

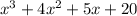
you just have ti group and search for a term in common that could help you factorize into two separated terms, first, you try and factorize the first two terms:

`x^(3)+4x^(2)  \\x^(2) (x+4)`

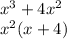
Remember always trying to take out the maximum exponential possible, in this case we were able to withdraw the
`x^(2)` and this helps us to factorize easier the second one since we already have a term that we want to have in common whic wuold be (x+4):

`5x+20\\5(x+4)`

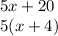
Now we just put together the
`x^(2)` and the 5, and we multiply it by our common factor:

`(x^(2) +5)(x+4).`