Answer:
x = 25
Step-by-step explanation:
We can let an arbitrary rectangle has a length and width of 10, making the total area 10*10 or 100. We know that the length of the rectangle is reduced by 10%, meaning the new length is now 10 - (0.1*10), or 9. The actual width is unknown, but we do know that it will be an x% reduction of the original width: 10 - (0.01x*10), or 10 - 0.1x. We are also given that the area is reduced by 32.5%. This means the new area is 100 - (0.325*100), or 100 - 32.5, which is 67.5. Now, we can use the area formula (length*width) to find the value of x:
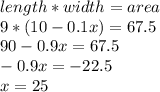
This means that the value of x is 25, or the width was reduced by 25%