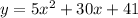Question

The function below is written in vertex form or intercept form. Rewrite them in standard form and show your work.

y = 5(x+3)^2-4

Answer 1

Answer: The standard form of equation will be

`f(x)=5x^2+30x+41`

Explanation:

Since we have given that

The vertex form of equation is given by

`y=5(x+3)^2-4`

We need to find the standard form :

Standard form is written as :

`f(x)=ax^2+bx+c`

So, our equation becomes,

`y =5(x+3)^2-4\\\\y=5(x^2+9+6x)-4\\\\y=5x^2+45+30x-4\\\\y=5x^2+30x+41`

Hence, the standard form of equation will be

`f(x)=5x^2+30x+41`

Answer 2

The standard form as
`y=5x^2+30x+41`

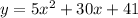
Explanation:

Given: A function which is written in vertex form or intercept form.

We have to re-write it in standard form that in terms of

Given
`y = 5(x+3)^2-4`

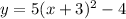
Squaring using
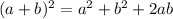`(a+b)^2=a^2+b^2+2ab` , we get,

`y=5(x^2+9+6x)-4`

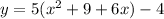
Multiply 5 inside , we get,

`y=5x^2+45+30x-4`

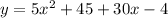
Solving further , we get,

`y=5x^2+30x+41`

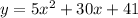
Thus , we have obtained the standard form as
`y=5x^2+30x+41`