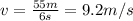Question

A lead ball is dropped into a lake from a diving board 5m above the water . It hits the water with a certain velocity and then sink with constant velocity in bottom . It reaches the bottom 5 second after it is dropped If g= 10m/s2 . Find depth of the lake and average velocity of the ball ?

Answer 1

1. Depth of the lake: 50 m

Step-by-step explanation:

The first part of the problem can be solved by using conservation of energy.

When it is dropped, all the mechanical energy of the ball is potential energy, given by:

`U=mgh`

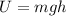
where m is the mass, g is the gravitational acceleration and h is the height.

When the bal hits the water, all the mechanical energy has been converted into kinetic energy:

`K=(1)/(2)mv^2`

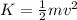
where m is the mass and v is the speed. Equalizing the two terms, we have:

`mgh=(1)/(2)mv^2\\2gh=v^2\\v=√(2gh)=√(2(10 m/s^2)(5 m))=10 m/s`

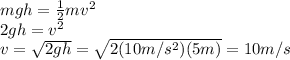
Then the ball travels in the water, keeping this constant velocity, for t=5 s. So, the total distance traveled underwater (which is the depth of the lake) is

`d=vt=(10 m/s)(5 s)=50 m`

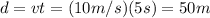
2. Average velocity: 9.2 m/s

Step-by-step explanation:

The average velocity during the whole path of the ball is equal to the ratio between the total distance traveled and the total time taken:

`v=(d)/(t)`

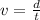
We already know the total distance: 5 meters above the water and 50 m underwater, so

d = 5 m + 50 m = 55 m

For the total time, we need to calculate the time spent above the water, which is given by

`S=(1)/(2)gt_a^2\\t_a = \sqrt{(2S)/(g)}=\sqrt{(2(5 m))/(10 m/s^2)}=1 s`

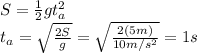
So the total time is: 1 second above the water + 5 seconds underwater:

t = 1 s + 5 s = 6 s

Therefore, the average velocity is

`v=(55 m)/(6 s)=9.2 m/s`