Question

The prism-shaped roof has equilateral triangular bases. Create an equation that models the height of one of the roof's triangular bases in terms of its sides. In your final answer, include all necessary calculations.

Answer 1

Copy and Paste Version

ADsqaured = ABsquared - BDsquared

ADsqaured = ABsquared - (1/2AB squared) 2

AD squared = 3/4AB squared

AD = square root 3/2 AB

​Now we can find the height of any of the bases

Explanation:

Answer 2

Answer: The answer is given below.

Step-by-step explanation: As shown in the attached figure, the prism-shaped roof has equilateral triangular bases, one of which is ΔABC. We need to create an equation that models the height of one of the roof's triangular bases in terms of its sides. Let ii be AD.

SEe the figure attached herewith, ΔABC forms an equilateral triangle, in which AD is the height. So, D will be the mid-point of BC and ∠ADB = ∠ADC = 90°.

Now, in ΔADB, we have

`AD^2=AB^2-BD^2\\\\\\\Rightarrow AD^2=AB^2-\left((1)/(2)AB^2\right)^2\\\\\\\Rightarrow AD^2=(3)/(4)AB^2\\\\\\\Rightarrow AD=(\sqrt 3)/(2)AB.`

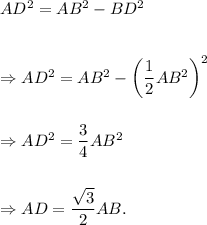
Thus, with the help of this model, we can find the height of any one of the roof's triangular bases.