Answer:
Perpendicular:

Parallel:

Explanation:
So when two lines are perpendicular, that means the the slope is the reciprocal with the opposite sign so:
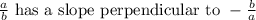 . In this case we have the equation in slope-intercept form, so it's easy to determine the slope, it's 3. So that means the perpendicular line will have a slope of:
. In this case we have the equation in slope-intercept form, so it's easy to determine the slope, it's 3. So that means the perpendicular line will have a slope of:
 . Since you have a slope of 3/1 which becomes 1/3 and also an opposite sign. This gives you the equation:
. Since you have a slope of 3/1 which becomes 1/3 and also an opposite sign. This gives you the equation:
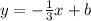 . We can solve for b, by plugging in a coordinate it passes through. This is given in the problem, with it being (4, 5) = (x, y). So plugging these values in as (x, y) gives you the equation:
. We can solve for b, by plugging in a coordinate it passes through. This is given in the problem, with it being (4, 5) = (x, y). So plugging these values in as (x, y) gives you the equation:
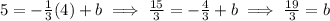 . This gives you the complete equation:
. This gives you the complete equation:

So when two lines are parallel, that means they have the slope, and a different y-intercept. This is because if they had the same y-intercept, then the two lines would be the same exact line. We already know the slope, it's 3. So we have the general equation:
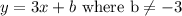 . The restriction on b, was explained on the previous sentence, if b=-3, then we have the same equation, which is not parallel, they would be the same line, meaning they would intersect at infinite points, which is completely different than two lines that never intersect. So now we can plug in the given point (4, 5) to solve for b. Plugging these coordinates in gives you:
. The restriction on b, was explained on the previous sentence, if b=-3, then we have the same equation, which is not parallel, they would be the same line, meaning they would intersect at infinite points, which is completely different than two lines that never intersect. So now we can plug in the given point (4, 5) to solve for b. Plugging these coordinates in gives you:
 . This gives you the complete equation:
. This gives you the complete equation:
