Question

What is the image of R for a dilation with center (0, 0) and a scale factor of 1 1/2? (6, -3) (2, -1/2) (2, 1) (6, -3/2)

Answer 1

The image of R=(4,-2) for a dilation with center (0, 0) and a scale factor of 1 1/2 is: First option (6,-3)

Explanation:

The image of a point P=(x,y) for a dilation with center at the origin O=(0, 0) and a scale factor of f is: P'=(f*x,f*y).

In this case the point is R=(4,-2)=(x,y)→x=4, y=-2

And the scale factor is:

`f=1(1)/(2)=(1(2)+1)/(2)=(2+1)/(2)\\ f=(3)/(2)`

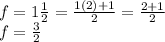
Then the image of point R=(4,-2) for a dilation with center at the origin O=(0,0) and a scale factor of f=1 1/2=3/2 is:

`R'=(f.x,f.y)\\ R'=((3)/(2)(4),(3)/(2)(-2))\\ R'=((3(4))/(2),(3(-2))/(2))\\ R'=((12)/(2),(-6)/(2) )`

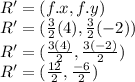
R'=(6,-3)