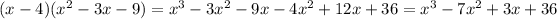Answer:
1)

2)
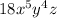
3)
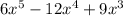
4) 40
5)
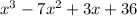
Explanation:
1) Distribute the negative sign that is outside the parentheses and then you must add like terms, as following:

2) According to the Product property of exponents, when you multiply powers with the same base, you must add the exponents. Then:
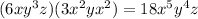
3) Apply the Distributive property and the Product property of exponents. Then, you obtain:
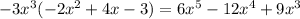
4)
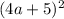 is a square of a sum, then, by definition you have:
is a square of a sum, then, by definition you have:
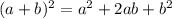
Then:
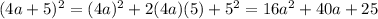
The coefficient of the second term is the number in front of the variable a. Then, the answer is: 40
5) Apply the Distributive property and the Product property of exponents, then, oyou must add the like terms: