Question

8. MAGAZINES You want to compare the number of words per sentence in a sports magazine to the number of words per sentence in a political magazine.

a. The data represent random samples of 10 sentences in each magazine. Compare the samples using measures of center and variation. Can you use this to make a valid comparison about the magazines? Explain.
Sports magazine: 9, 21, 15, 14, 25, 26, 9, 19, 22, 30 Political magazine: 31, 22, 17, 5, 23, 15, 10, 20, 20, 17

Answer 1

I also don't know so I am sorry I need point

Answer 2

On comparing the center i.e. mean we get that the sports magazine 19 uses more words than a political magazine 18 but they are almost the same because their difference is only 1. The variance of sports magazines 5.8 is greater than the variance of political magazines 5.2. We cannot use this to make a valid comparison about the magazines to a magazine the content matters or maybe the number of readers matters not the number of word count.

Explanation:

Given: The number of words per sentence in a sports magazine to the number of words per sentence in a political magazine. The data represent random samples of 10 sentences in each magazine.

Sports magazine
`$$9,21,15,14,25,26,9,19,22,30$$`.

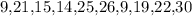Political magazine
`$$31,22,17,5,23,15,10,20,20,17$$`.

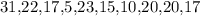To compare the samples using measures of center and variation.

• Find the mean of both the data and compare them.
• Find the variance of both the data and compare them.

Step 1 of 2

The mean of the words of sports magazine is
`\begin{aligned}(9+21+15+14+25+&26+9+19+22+30) * (1)/(10) \\&=(190)/(10) \\&=19\end{aligned}`

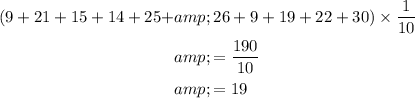
The mean of the words of the political magazine is
`\begin{aligned}&(31+22+17+5+23+15+10+20+20+17) * (1)/(10)\\&=(180)/(10)\\&=18\end{aligned}`

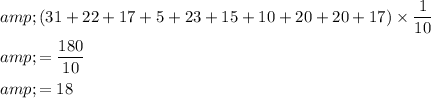
On comparing the center i.e. mean we get that the sports magazine uses more words than a political magazine.

Step 2 of 2

Variation of sports magazine is
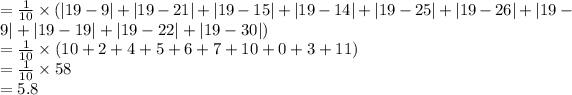`=(1)/(10)*(|19-9|+|19-21|+|19-15|+|19-14|+|19-25|+|19-26|+|19-9|+|19-19|+|19-22|+|19-30|)$$\\ $$=(1)/(10)*(10+2+4+5+6+7+10+0+3+11)$$\\$$=(1)/(10)*58$$\\$$=5.8$$`Variation of the political magazine is \end{tabular}

`=(1)/(10)*(|18-31|+|18-22|+|18-17|+|18-5|+|18-23|+|18-15|+|18-10|+|18-20|+|18-20|+|18-17|)$$\\ $$=(1)/(10)*(13+4+1+13+5+3+8+2+2+1)$$\\ $$=(52)/(10)$$\\ $$=5.2$$`

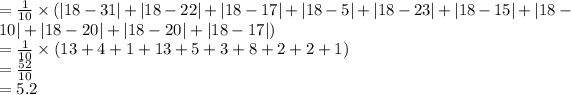
The variance of sports magazines is greater than the variance of political magazines.

We cannot use this to make a valid comparison about the magazines to a magazine the content matters or maybe the number of readers matters not the number of word count.