Answer:
The given lines are perpendicular.
Explanation:
In the question, two lines are given as line 1 passes through (1,7) and (5,5). Whereas, line 2 passes through (-1,-3) and (1,1).
It is required to find the slope of given lines and figure out whether they are perpendicular, parallel or neither.
To solve this question, first find the slope of both lines. Check if their product is equal to -1, then they are perpendicular. If the slopes are equal the lines are parallel.
Step 1 of 2
Find the slope of first line.
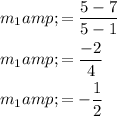
Step 2 of 2
Find the slope of first line.

And
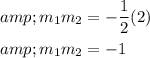
Since, both slopes are reciprocal of each other.
Therefore, the lines are perpendicular.