Answer:
2 pounds of coffee costing $4 should be mixed with 3 pounds of coffee costing 4.50 a pound to obtain a mixture costing $4.30 a pound.
Explanation:
Given that coffee costing $4 a pound mixed with 3 pounds of coffee costing $4.50 a pound . we have to find the number of pounds of coffee mixed with 3 pounds of coffee costing $4.50 a pound to obtain a mixture costing $4.30 a pound.
Let x be the pounds of coffee mixed.
Cost of coffee of 3 pounds costing $4.50 a pound is 3(4.50)=$13.5
Total weight of mixture=x+3
The cost per pound of the mixture will be the total value of the coffee in the mixture divided by the total weight of the mixture which is 4x+13.5 divided by total weight 3 + x.
∴ A/Q the equation becomes
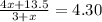
⇒ 4x+13.5=4.30(3)+4.3x
⇒ 0.6=0.3x
⇒ x=2
Hence, 2 pounds of coffee costing $4 should be mixed with 3 pounds of coffee costing 4.50 a pound to obtain a mixture costing $4.30 a pound.