Answer:
(d) Gauss-Jordan Elimination
80 carnations; 50 roses; 70 daisies
Explanation:
The given relations can be written as equations, which can be expressed as one matrix equation. Any of the methods listed can be used to solve the matrix equation.
Equations
If we let c, r, d represent numbers of carnations, roses, and daisies ordered, respectively, then the given relations can be written as ...
c + r + d = 200 . . . . . . 200 flowers were ordered
0c -r +d = 20 . . . . . . . . . . . . . 20 more daisies than roses were ordered
1.50c +5.75r +2.60d = 589.50 . . . . . the total value of the order
Matrix Equation
Written as a matrix equation, it will be of the form ...
AX = B
where A is the square matrix of variable coefficients, X is the column vector of variables, and B is the column vector of equation right-side constants. This is the matrix equation:
![\left[\begin{array}{ccc}1&1&1\\0&-1&1\\1.50&5.75&2.60\end{array}\right] \left[\begin{array}{c}c\\r\\d\end{array}\right] =\left[\begin{array}{c}200\\20\\589.50\end{array}\right]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/fspgu3w4re6gjtf88s7x.png)
Solution Methods
The mathematical operations required to find the equation solution can be briefly described as ...
Inverse Matrices
The coefficient matrix is inverted and multiplied by the constant column vector:
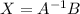
The inversion operation requires computation of 10 determinants, of which 9 are of 2×2 matrices. That's a total of about 39 multiplications, 9 divisions, and 20 additions.
Cramer's Rule
Using Cramer's rule requires computation of 4 determinants of 3×3 matrices. The total number of operations comes to about 48 multiplications, 3 divisions, and 20 additions.
Gaussian Elimination
To obtain the upper triangular matrix that results from Gaussian Elimination requires about 11 multiplications, 11 additions, and 2 divisions. This finds the value of one variable, but the others must be found by substitution into the remaining two equations, requiring an additional 3 multiplications and 3 additions.
Gauss-Jordan Elimination
This method starts with an augmented matrix that appends column vector B to the square matrix A. The result of this is shown in the attachment. It is a diagonal matrix with the variable values a direct result of the matrix operations. The calculator's RREF( ) function performs matrix row operations to transform the augmented matrix to this Reduced Row-Echelon Form. About 6 multiplications, 6 additions, and 4 divisions are required.
Clearly, Gauss-Jordan Elimination is the method that requires the least computational work, so it would probably be used for this question.
Flowers
The attachment shows the order to be ...
- 80 carnations
- 50 roses
- 70 daisies
__
Additional comment
The estimates of computational load presented by each of the solution methods are not intended to be exact counts. For this specific problem, some of the operations can be avoided due to the fact that some coefficients are already 1. Also, some computations are not needed simply because they are intended to produce an outcome that is already known. The intention is to give an idea of the relative difficulty of using these different methods.
In some cases, computationally less-efficient methods may be preferred because they are simpler to describe.