Answer:
The roots of the polynomial equation are:
-1,3+2i and 3-2i
Explanation:
We are given a polynomial equation as:

this equation could also be written as:
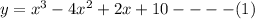
and
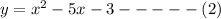
Now if this equation has a complex root as:
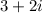
and we know that for any polynomial equation witth real coefficients the complex roots always appear in pair.
if a+ib is some root of a polynomial equation with real coefficients then its conjugate a-ib is also a root of the equation.
Hence, the other root of this polynomial equation will be:

Now we will graph these system of equations i.e. equation (1) and equation (2).
on solving the equation we have:
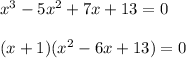
(since
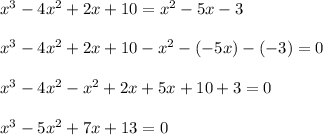
)
Hence on solving the equation we have:
x=-1,3+2i and 3-2i are the roots of the equation.