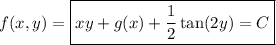Multiply both sides by
 to get an exact equation.
to get an exact equation.
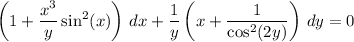
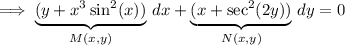
This ODE is exact since
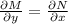 . Then the solution is given by an implicit function
. Then the solution is given by an implicit function
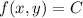
Taking differentials on both sides by the chain rule gives
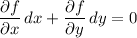
so that we have the system of partial differential equations
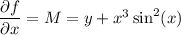
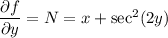
Integrate both sides of the first of these equations with respect to
 to recover
to recover
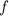 .
.
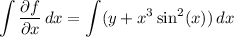
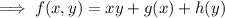
where
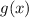 is the antiderivative of
is the antiderivative of
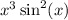 (and is easy enough to compute by parts).
(and is easy enough to compute by parts).
Differentiating both sides with respect to
 gives
gives
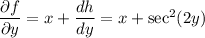
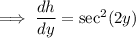
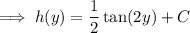
Then the general solution to the ODE is