Question

A chemist needs to make 30 ounces of a 25% alcohol solution by mixing together a 15% alcohol solution with a 40% alcohol solution. How much of each solution do they need to use? Explain.

Answer 1

The use of 15% solution be 18 ounce and the use of 40% solution be 12 ounce .

Explanation:

Let us assume that the use of 15% solution be x .

Let us assume that the use of 40% solution be y .

As given

A chemist needs to make 30 ounces of a 25% alcohol solution by mixing together a 15% alcohol solution with a 40% alcohol solution.

Equation becomes

x + y = 30

25 % is written in the decimal form .

`= (25)/(100)`

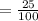
= 0.25

15 % is written in the decimal form .

`= (15)/(100)`

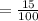
= 0.15

40 % is written in the decimal form .

`= (40)/(100)`

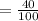
= 0.40

Equation becomes

0.15x + 0.40y = 30 × 0.25

`(15x)/(100) + (40)/(100) = (30* 25)/(100)`

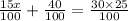
Simplify the above

15x + 40y = 750

Two equations are

x + y = 30

15x + 40y = 750

Multiply x + y = 30 by 15 and subtracted from 15x + 40y = 750.

15x - 15x + 40y - 15y = 750 - 450

25y = 300

`y = (300)/(25)`

y = 12

Puttiny the value of y in the x + y = 30 .

12 + x = 30

x = 30 - 12

x = 18

Therefore the use of 15% solution be 18 ounce and the use of 40% solution be 12 ounce .