Question

How many 3 digit numbers have the following property: Non-negative difference of any two neighboring digits is more than 8?

Answers can be 8, 6, 7, 9, 10

Answer 1

7 maybe? (I'm assuming any two neighboring digits is greater than or equal to 8)

Explanation:

Ok so it's important to establish which combinations of numbers have a difference of 8+. The most obvious one is (0, 8), and (1, 9), but there's also (0, 9). In my explanation I'll express a three digit number as:
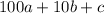`100a+10b+c` where a, b, and c will form the three digit number. It's important to understand that:
`a\\e0`, because if it was 0, then it would be a two digit number, because there would be no hundreds place. So let's start with the (0, 8) combination. a=8 and b=0, and c can have 2 different values. So we get the two numbers:
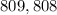`809, 808`. Now let's using the (1, 9) which can be rearranged where (a=1, b=9) OR (a=9, b=1) since this combination doesn't have a 0 as one of the values. So let's start with a=1, b=9, this leaves 2 values for c. This gives you the numbers:
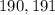`190, 191`. Now let's use the a=9, b=1 combination. This only leaves 1 values for c since 8-1 = 7, meaning c can only equal 9. This gives you the following number:
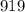`919`. Now for the last combination: (0, 9). In this combination a has to be 9, and b has to be 0. This gives you 2 values for c. This gives you the following two numbers:
`909, 908`. Combining all these numbers we get the following numbers:
`909, 908, 919, 809, 808, 190, 191`