Answer:
In Alex expression,
 shows the number of Amoeba after h hours.
shows the number of Amoeba after h hours.
Where,
 is the growth factor for h hours.
is the growth factor for h hours.
Let,
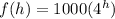
Initially, h = 0 ⇒ f(0) = 1000
Hence, 1000 shows the initial number of amoeba,
Now, after 1 hours, h = 1,
⇒ Number of amoeba, f(1) = 1000 × 4
For h = 2, number of amoeba, f(2) = 1000 × 4 × 4
For h = 3, number of amoeba, f(3) = 1000 × 4 × 4 × 4
..........so on...
⇒ Number of amoeba is increasing with the growth factor 4,
4 is the growth factor by with number of amoeba is increasing.
Now, in Emma expression,
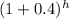 shows the number of amoeba after h hours,
shows the number of amoeba after h hours,
Let,
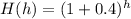
Initially, h = 0 ⇒ H(0) = 1
Initial number of amoeba = 1,
Now, after h = 1,
H(1) = (1+0.4)
For h = 2, H(2) =
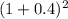 = 1 (1+0.4)(1+0.4)
= 1 (1+0.4)(1+0.4)
For h = 3, H(3) =
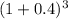 = 1 (1+0.4)(1+0.4)(1+0.4)
= 1 (1+0.4)(1+0.4)(1+0.4)
...... so on,...
Hence, the number of amoeba is increasing with the rate of 0.4 and with the growth factor of (1+0.4).
0.4 is the growth rate.
And, (1+0.4) is the growth for each hour.