Question

ABCD is a parallelogram. Find m ∠D. Enter the answer as a number.

ABCD is a parallelogram. Find the measure of AB. Enter the answer as a number.
ABCD is a parallelogram. Find m ∠C. Enter the answer as a number.

Answer 1

`m\angle D=144^o`

`AB=30`

`m\angle C=36^o`

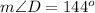
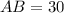
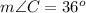
Explanation:

We have been given that ABCD is a parallelogram.

A. Since we know that consecutive angles of parallelogram are supplementary.

We can set an equation as:

`m\angle A+m\angle D=180^o`

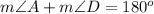
Upon substituting measure of angle A in our equation we will get,

`36^o+m\angle D=180^o`

`36^o-36^o+m\angle D=180^o-36^o`

`m\angle D=144^o`

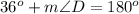
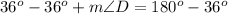
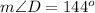
Therefore, measure of angle D is 144 degrees.

B. Since we know that opposite sides of parallelogram are of equal length.

We can see that side CD is the opposite side of side AB and measure of side CD is 30, therefore, the measure of side AB is 30.

C. Since we know that opposite angles of parallelogram are of equal measure.

We can see that angle A is the opposite angle of angle C and measure of angle A is 36 degrees.

`m\angle C=m\angle A;\text{ Opposite angles of parallelogram are of equal measure}`

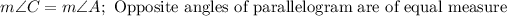
Upon substituting angle A's measure in our equation we will get,

`m\angle C=36^o`

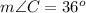
Therefore, measure of angle C is 36 degrees.