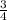Question

What is the slope of (8,3) and (-4,-6)?

Answer 1

Answer: The slope of the line formed by these two points is
`(3)/(4)`

Explanation:

To calculate the slope, we use the formula:

`Slope=(y_2-y_1)/(x_2-x_1)`

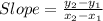
For the coordinates given:

`x_1=8\\y_1=3\\x_2=-4\\y_2=-6`

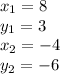
Putting values in above equation, we get:

`Slope=((-6-3))/((-4-8))\\\\Slope=(-9)/(-12)\\\\Slope=(3)/(4)`

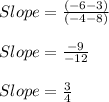
Hence, the slope of the line formed from these two coordinates is
`(3)/(4)`