Question

Explain how to determine which numbers must be excluded from the domain of a rational expression. Please provide an example with your explanation.

Answer 1

• When we are having a rational expression i.e. a expression of the type:

`(f(x))/(g(x))`

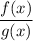
Where f(x) and g(x) are polynomial functions.

Now the domain of this rational expression is whole of the real numbers except the points where the function g(x) will be zero.

Hence we have to exclude the points where the given denominator quantity is zero.

• Let us consider an example as:

Let R(x) denote the rational function as:

`R(x)=(x^2)/((x-2)(x-3))`

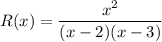
Now the domain of this rational function will be whole of the real line minus the points where the denominator is zero.

We know that (x-2)(x-3) is zero when x=2 or x=3.

Hence, the domain of R(x) is: R- {2,3}.