Answer:
C.

Explanation:
We have been given an equation
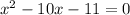 . We are asked to choose the equation which has the same solutions as the given equation from our given choices.
. We are asked to choose the equation which has the same solutions as the given equation from our given choices.
Upon looking at our given choices we can see that they are in form of perfect square, so we will complete the square for our given equation.

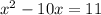
Now we will add the square of
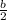 to both sides of our equation.
to both sides of our equation.
We can see from our given equation that the value of b is 10.
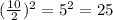
Adding 25 on both sides of our equation we will get,
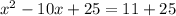
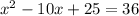
Upon writing left side of our equation as a perfect square we will get,

Therefore, the equation
 has the solutions as the given equation and option C is the correct choice.
has the solutions as the given equation and option C is the correct choice.