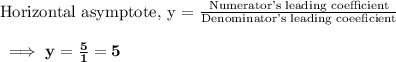Question

Which is a graph of f(x)=5x-2/x+2,with any vertical or horizontal asymptotes indicated by dashed lines?

Answer 1

B on edge

Explanation:

Answer 2

The graph of the given function f(x) is attached below :

`f(x)=(5\cdot x -2)/(x+2)`

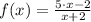
To find vertical asymptotes :

Since the given function is rational so the vertical asymptotes of the function will be zeroes of the denominator

Vertical Asymptotes : x + 2 = 0

⇒ x = -2

To find horizontal asymptotes :

As the degree of numerator is s equal to the degree of denominator. Therefore,

`\text{Horizontal asymptote, y = }\frac{\text{Numerator's leading coefficient}}{\text{Denominator's leading coeeficient}}\\\\\bf\implies y = (5)/(1)=5`