If
 is the first number in the progression, and
is the first number in the progression, and
 is the common ratio between consecutive terms, then the first four terms in the progression are
is the common ratio between consecutive terms, then the first four terms in the progression are
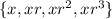
We want to have
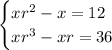
In the second equation, we have

and in the first, we have

Substituting this into the second equation, we find
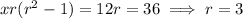
So now we have
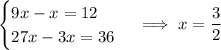
Then the four numbers are
