Question

Find the zero of each function and state the multiplicity of each zero. Please show all steps.

1. y=(x+3)^3


2. y=(x-2)^2(x-1)


3. y=(2x+3)(x-1)^2

Answer 1

1. y=(x+3)^3. Zero: x=-3 multiplicity 3.

2. y=(x-2)^2 (x-1). Zeros: x=2 multiplicity 2; x=1 multiplicity 1.

3. y=(2x+3)(x-1)^2. Zeros: x=-3/2 multiplicity 1; x=1 multiplicity 2.

Explanation:

1. y=(x+3)^3

`y=0\\ (x+3)^3=0\\ \sqrt[3]{(x+3)^3}=\sqrt[3]{0}\\ x+3=0\\ x+3-3=0-3\\ x=-3`

Zero: x=-3 multiplicity 3.

2. y=(x-2)^2 (x-1)

`y=0\\ (x-2)^2(x-1)=0\\ \left \{ {{(x-2)^2=0} \atop {x-1=0}} \right\\ \left \{ {{√((x-2)^2) =√(0) } \atop {x-1+1=0+1}} \right\\ \left \{ {{x-2=0} \atop {x=1}} \right\\ \left \{ {{x-2+2=0+2} \atop {x=1}} \right\\ \left \{ {{x=2} \atop {x=1}} \right.`

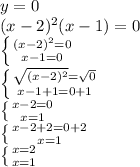
Zeros: x=2 multiplicity 2; x=1 multiplicity 1

3. y=(2x+3)(x-1)^2

`y=0\\ (2x+3)(x-1)^2=0\\ \left \{ {{2x+3=0} \atop {(x-1)^2=0}} \right\\ \left \{ {{2x+3-3=0-3} \atop {√((x-1)^2) =√(0) }} \right\\ \left \{ {{2x=-3} \atop {x-1=0}} \right\\ \left \{ {{(2x)/(2) =(-3)/(2) } \atop {x-1+1=0+1}} \right\\ \left \{ {{x=-(3)/(2) } \atop {x=1}} \right.`

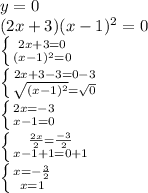
Zeros: x=-3/2 multiplicity 1; x=1 multiplicity 2.